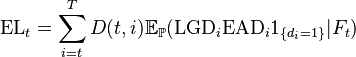Expected Loss
Definition
Expected Loss (EL) is a key credit risk parameter which assigns a numerical value between zero and one (a percentage) denoting the expected (anticipated) financial loss upon a credit related event (default, bankruptcy) within a specified time horizon. Multiplying the percentage with the exposure provides the expected loss in monetary terms.
From a statistical perspective expected loss corresponds to the mean (average) of a Loss Distribution Function and is assessed on the basis of the historical loss experience (see also Unexpected Loss). Such losses, because they are expected, are provided for in the pricing of credits, with poorer credits attracting higher risk-spreads (and possibly other requirements to mitigate the credit risk such as collateral for instance) since their Probability of Default and their potential for Loss Given Default are higher.
Credit risk spreads theoretically provide the basis for provisions for credit losses or loan loss reserves. Under older accounting and tax rules, most banks only set aside provisions/loss reserves on assets when the risk was clearly identified, only capturing part of the losses that can be expected over a loan portfolio’s time horizon.
The notion of expected loss has general applicability but it is adopted concretely and has very specific definition and meaning in
- Regulatory Expected Loss under the Basel II/III standards[1]
- Expected Credit Loss under IFRS 9 / CECL [2]
In regulatory context EL means the ratio of the amount expected to be lost on an exposure from a potential default of a counterparty or dilution over a one year period to the amount outstanding at default[3]
Formula
Conceptually the expected definition is captured in the following mathematical expression
- Where t is the date at which the expected loss is calculated
- T is the Expected Life of the instrument
- i denotes possible times of default / loss (normally associated with instrument cashflows)
- di is the random (unknown) event of default at time i
- LGD denotes Loss Given Default
- EAD denotes Exposure at Default
- D(t,i) denotes the discount rate at time t (based on the Effective Interest Rate, for the different cashflow maturities i
- Ft denotes the subjective or market based information set used formulate the estimate at time t
- P denotes the subjective or market based assignment of default probabilities to the events di
Issues and Challenges
- Multiple competing paradigms for estimation (from historical data, bond spreads, credit default derivatives spread)
- Requires a Term Structure for a complete view on credit risk
- Sensitive to the Default Definition and the Loss Given Default assumptions
See Also
- Expected Credit Loss / Lifetime Expected Credit Losses for accounting perspectives and formulas
- Probability of Default
- Regulation (EU) 575/2013 Art 5(3)