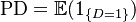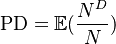Probability of Default
Contents
Definition
The Probability of Default (PD) is the probability of an Obligor defaulting (Credit Event) on some obligation.
The Probability of Default is a key risk parameter used in the context of Credit Risk management. It is a forward-looking Expectation Measure, which assigns a numerical value between zero and one to the likelihood of an appropriately defined Credit Event (such as default, bankruptcy), within a specified time horizon.
In the Internal Ratings-Based Approach the probability of default of a counterparty is estimated over a one year period[1]
Information Content
A probability of default metric encapsulates two types for information[2]
- Aggregate, Macro, Non-obligor specific information. This is information observable at the time of PD estimation that is shared (is common) by many borrowers. This category typically includes Macroeconomic Factors such as exchange rates, GDP growth rates etc.
- Borrower-specific, Idiosyncratic information. This is the information that is unique to a particular obligor. Such information may be static, such as an obligor’s line of business, country of incorporation, or it may be more dynamic in character, such as an obligor’s leverage ratio, country of operation, market share etc.
These two types of information are not necessarily uncorrelated, especially over longer periods. For example valuations in asset markets may affect leverage both directly and via management induced leverage changes.
Usage and Mathematical Formulation
There are two primary modes of using the Probability of Default measure.
- In the measurement of credit risk associated with an individual entity, in which instance the PD is an expectation of a single default event
- In the measurement of credit risk associated with a pool of similar entities in which instance the PD is an expected Default Rate
For a single entity the probability of default is defined as the likelihood that there is a credit event (Indicated by a Random variable, D that takes the value D=0 if there is no event and the value D=1 if there is a credit event:
For pooled assets that are not modelled individually, the probability of default is defined as the expected default rate (indicated by the fraction of defaulted over total assets
Issues and Challenges
- There are multiple competing paradigms for the estimation of probability of default with no single best approach for all contexts
- A Term Structure rather than a single point estimate is more appropriate for complete view on credit risk
- The estimate is sensitive to the Default Definition
See Also
References
Disclaimer
This entry annotates a FIBO Ontology Class. FIBO is a trademark and the FIBO Ontology is copyright of the EDM Council, released under the MIT Open Source License. There is no guarantee that the content of this page will remain aligned with, or correctly interprets, the concepts covered by the FIBO ontology.
| IsDefinedBy URI of an entity that is defined via an imported vocabulary. | https://spec.edmcouncil.org/fibo/ontology/FND/RiskExt/Risk/index-en.html + |