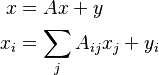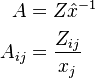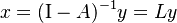Leontief Model
Contents
Definition
A Leontief Model is an economic model following the proposals of economist Wassily Leontief who developed a system of economic analysis (Input-Output Model) in the 1930s and 1940s. It is based on a linear economy assumption and demand-style economic modeling[1]
Formula
Starting with the Market Balance or Total Output equation:
where
- x is the column vector of output of endogenous accounts
- y the column vector of Final Demand and
A is the so-called Technical Coefficient Matrix, whose elements are the elements of the Transactions Matrix divided by the total of their corresponding output column:
The Leontief inverse matrix 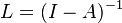 is obtained, satisfying the condition
is obtained, satisfying the condition 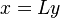 .
.
with 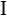 defined as the identity matrix (Kronecker delta) with dimension equal to the size of A.
defined as the identity matrix (Kronecker delta) with dimension equal to the size of A.
Interpretation
In the demand-driven, upstream or Leontief model, a matrix of direct requirements 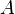 is defined as the inter-industrial flows
is defined as the inter-industrial flows 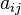 from an industry i to an industry j per gross output of sector j.
from an industry i to an industry j per gross output of sector j.
An element 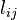 of the total requirements matrix, or Leontief inverse, L represents the amount of gross output from sector i that was produced to satisfy a unit of final demand y from sector j.
of the total requirements matrix, or Leontief inverse, L represents the amount of gross output from sector i that was produced to satisfy a unit of final demand y from sector j.
Usage
An important goal of IO analysis is to examine the interdependencies between production and consumption within an economy. Such analysis includes the flow of goods of services between the economy and the rest of the world and can be expressed in monetary or other measurement units.