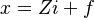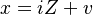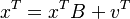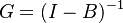Ghosh Model

Definition

A Ghosh Model is a category of Supply Side Input–Output Models that represent an alternative type of Input-Output Model to the more commonly used demand side Leontief Model.

The two categories of models are based on the same set of economic data^[1] but interpret and use them differently.

Structure

Contrary to the static IO quantity model, the static IO price model (or Gosh model) is downstream oriented. It captures the effects of input factors, such as wages, on sectoral production prices. As such, they assume that cost/price changes are passed on completely and directly (cost push/through). The price model is not relevant in the context of classical EIA and EEIO analyses.

The Ghosh Model approach is made operational by essentially transposing the vertical (column) view of an Input-Output model to a horizontal (row) one. Instead of dividing each column of Primary Input 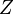$Z$ by the gross output of the sector associated with that column, the suggestion is to divide each row of Z by the gross output of the sector associated with that row.

If we denote by 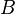$B$ the direct-output coefficients matrix that results, these 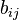$b_{ij}$ coefficients represent the distribution of sector i’s outputs across sectors j that purchase inter-industry inputs from i. These are frequently called allocation coefficients, as opposed to technical coefficients.

Formula

The model uses the same quantities that underpin the demand-driven model, namely Z, f, and v, from which x follows as

x = Z i + f

or, as,

x = i Z + v

x^{T} = x^{T} B + v^{T}

where v is Value Added or primary factors and B is the distribution coefficients matrix, calculated by the elements of the SAM divided by the total of their corresponding row. The Ghosh multipliers matrix is derived as

G = (I - B)^{-1}

In the downstream or Ghosh model, a matrix of direct sales A, is defined as the inter-industrial flows from an industry i to an industry j per gross input of i.

An element of the total sales matrix, or Ghosh inverse, represents the amount of gross input into industry j that absorbed, or utilised a unit of primary inputs v into industry i.

Further Resources

References

↑ R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009

[1] R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009

[1]