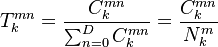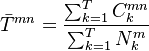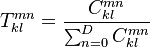Cohort Estimator
Contents
Definition
The Cohort Estimator is a simple frequentist estimation of multi-state transitions. The estimator can be used to derive the transition probability matrix of a Markov Chain process with a finite number of states.
Methodology
- Prerequisite for applying the approach is the definition of a suitable number of temporal cohorts and the allocation of all observed entities into such cohorts. The temporal intervals defining the cohorts are part of the design of the statistical analysis and depend on the domain.
- A second methodological aspect is the treatment of left/right censoring and transitions happening within a cohort interval. Multiple approaches are possible (first or last observed state within a cohort, average or longest living state etc.)
- Whether the different periods / cohort intervals can be consider homogeneous or not.
Single Period Cohort Estimator
In a single period cohort estimation all periods are considered equivalent (different samples of one-period transitions).
- The position in state space for an entity
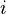 at discrete time
at discrete time 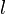 is a random variable
is a random variable 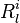 taking values in the state space
taking values in the state space 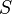 .
. - We assume a finite state space
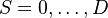
- Cohorts are defined by equal temporal intervals
![[t_{k-1}, t_{k}]](https://www.openriskmanual.org/wiki/images/mathdata/b/5/8/b588d2e8483f88eda5e54c35c07939a7.png)
- Let
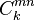 be the number (count) of entities at state
be the number (count) of entities at state 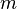 at time
at time 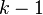 and at state
and at state 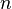 at time
at time 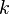 .
. - Let
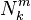 be the number (count) of all entities at state
be the number (count) of all entities at state 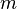 at time
at time 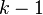 .
.
The directly estimated transition probability for that cohort is:
The estimator reflects that the probability of transition from m to n is the observed count number 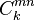 of all entities that migrated from m to n as a fraction of the count of all entities whose rating was m at k-1, that is,
of all entities that migrated from m to n as a fraction of the count of all entities whose rating was m at k-1, that is, 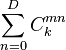 , irrespective of where they migrated to. The denominator includes all entities that did not migrate
, irrespective of where they migrated to. The denominator includes all entities that did not migrate 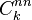 .
.
Count-Weighted Average
Under the assumption of homogeneity the estimates of different periods can be averaged. Using observation count as weights this results in an average transition matrix
NB: The count-weighted average will in general be different that the simple arithmetic average of estimated matrices over different periods.
Multi-Period Cohort Estimator
A multi-period estimator considers longer period intervals without the assumption of time-homogeneity. Computationally it is straight-forward extension:
where 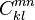 denotes the migration count of the period [k,l].
denotes the migration count of the period [k,l].
Confidence Intervals
Confidence intervals for the cohort estimator can be estimated using the multinomial proportions method[1]
Issues and Challenges
- State changes which occur within the period [k-1,k] are ignored. The time resolution (the number of cohorts) must be chosen so that there is as little ignored transition history as possible.
- The cohort estimator gives zero probability to a migration event that is not present in the data. E.g. in the presence of (right) censoring where we do not know what happens to the firm after the sample window closes (e.g. does it default right away or does it live on until the present) [2]
- Left truncation where firms only enter sample if they have either survived long enough or have received a rating.