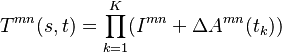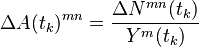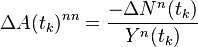Aalen-Johansen Estimator
Contents
Definition
The Aalen-Johansen estimator is a multi-state (matrix) version of the Kaplan–Meier estimator for the hazard of a survival process. The estimator can be used to estimate the transition probability matrix of a Markov process with a finite number of states. [1]
Estimator
The position in state space for an entity 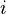 in continuous time
in continuous time 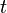 is a Random Variable
is a Random Variable 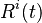 taking values in the state space S (We assume a finite state space
taking values in the state space S (We assume a finite state space 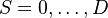 ).
).
The estimator is given by the expression
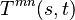 is the transition matrix element from time s to time t, the mn-th element of the matrix denotes the probability that the Markov process starting in state m at time s will be in state n at time t. The summation is over all times
is the transition matrix element from time s to time t, the mn-th element of the matrix denotes the probability that the Markov process starting in state m at time s will be in state n at time t. The summation is over all times 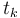 where transition events are observed (a total of K).
where transition events are observed (a total of K).
Off-diagonal elements
The estimation of the transition intensities 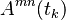 at any time
at any time 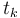 where transitions are observed is simply by counting:
where transitions are observed is simply by counting:
where 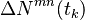 is the number of transitions observed from state m to state n at time
is the number of transitions observed from state m to state n at time 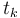 and
and 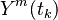 is the number of entities in state m right before time
is the number of entities in state m right before time 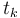
Diagonal elements
The diagonal elements are given by
where 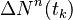 is the number of transitions away from state n at time
is the number of transitions away from state n at time 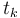
See Also
The Aalen-Johansen estimator is equivalent to the cohort method when the latter is applied to very short intervals
References
- ↑ Aalen, O. O. and Johansen, S. (1978). An empirical transition matrix for nonhomogeneous Markov chains based on censored observations. Scandinavian Journal of Statistics 5, 141–150.