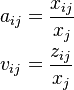Difference between revisions of "Input-Output Coefficient"
From Open Risk Manual
Wiki admin (talk | contribs) (Created page with "__SHOWFACTBOX__") |
Wiki admin (talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Definition == | ||
| + | '''Input-Output Coefficient''' (also technical coefficient) is any of the numerical elements of a symmetric [[Input-Output Matrix]]. | ||
| + | |||
| + | == Interpretation == | ||
| + | The input coefficients can be interpreted as the percentage share (%) of costs for [[Intermediate Input | intermediate inputs]] (goods and services) and [[Primary Input | primary inputs]] in [[Total Output]] (production value).<ref>R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009</ref> | ||
| + | |||
| + | == Formula == | ||
| + | The input-output coefficients, are calculated by dividing each value in the IO table by the corresponding column total (i.e., the production value). | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | a_{ij} & = \frac{x_{ij}}{x_j} \\ | ||
| + | v_{ij} & = \frac{z_{ij}}{x_j} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | where | ||
| + | |||
| + | * <math>a_{ij}</math> are the input coefficients for intermediate inputs, | ||
| + | * <math>v_{ij}</math> are the input coefficients for other primary inputs, | ||
| + | * <math>x_{ij}</math> is the flow of commodity i to sector j (transaction bloc of the IO table), | ||
| + | * <math>z_{ij}</math> is the flow of [[Primary Input]] i to sector j ([[Value Added]] bloc of the IO table) | ||
| + | * <math>x_j</math> is the output of sector j (production value). | ||
| + | |||
| + | == See Also == | ||
| + | * [[Input-Output Model]] | ||
| + | |||
| + | == Further Resources == | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=70 Crash Course on Input-Output Model Mathematics] | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=64 Introduction to Input-Output Models using Python] | ||
| + | |||
| + | |||
| + | == References == | ||
| + | <references/> | ||
| + | |||
| + | [[Category:EEIO]] | ||
| + | |||
| + | {{#set:Has Formula = HAS_FORMULA}} | ||
| + | |||
__SHOWFACTBOX__ | __SHOWFACTBOX__ | ||
Latest revision as of 18:17, 16 November 2023
Definition
Input-Output Coefficient (also technical coefficient) is any of the numerical elements of a symmetric Input-Output Matrix.
Interpretation
The input coefficients can be interpreted as the percentage share (%) of costs for intermediate inputs (goods and services) and primary inputs in Total Output (production value).[1]
Formula
The input-output coefficients, are calculated by dividing each value in the IO table by the corresponding column total (i.e., the production value).
where
-
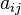 are the input coefficients for intermediate inputs,
are the input coefficients for intermediate inputs, -
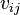 are the input coefficients for other primary inputs,
are the input coefficients for other primary inputs, -
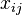 is the flow of commodity i to sector j (transaction bloc of the IO table),
is the flow of commodity i to sector j (transaction bloc of the IO table), -
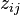 is the flow of Primary Input i to sector j (Value Added bloc of the IO table)
is the flow of Primary Input i to sector j (Value Added bloc of the IO table) -
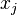 is the output of sector j (production value).
is the output of sector j (production value).
See Also
Further Resources
References
- ↑ R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009