Difference between revisions of "Incremental Default Probability"
From Open Risk Manual
Wiki admin (talk | contribs) (→Notation) |
Wiki admin (talk | contribs) |
||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
| − | The term '''Incremental Default Probability''' is used in the context of multi-period credit risk analysis to denote the likelihood that a legal entity is observed to ''have experienced'' a [[Credit Event]] during a defined period of time. | + | The term '''Incremental Default Probability''' is used in the context of multi-period credit risk analysis to denote the likelihood that a legal entity is observed to ''have experienced'' a [[Credit Event]] ''during a defined period of time''. |
| − | The incremental default probability can be considered as | + | The incremental default probability can be considered as another building block of the [[Credit Curve]], alternative to the [[Cumulative Default Probability]] representation. |
| − | |||
| − | |||
== Notation == | == Notation == | ||
| − | + | Observing whether an entity is defaulted over a period <math>[t_{k-1}, t_k]</math>, the incremental default probability is denoted <math>p_k</math>. Incremental default probabilities} during period k, given an initial rating of m, are denoted by | |
| − | Incremental default probabilities} during period k, given an initial rating of m, are denoted by | ||
:<math> | :<math> | ||
\mbox{PD}^{m}_{t,k} = p^m_k = 1_E [ 1_{\{ R_{k} = D \}} | F_t, R_0=m] = P(R_k=D | F_t, R_0=m) | \mbox{PD}^{m}_{t,k} = p^m_k = 1_E [ 1_{\{ R_{k} = D \}} | F_t, R_0=m] = P(R_k=D | F_t, R_0=m) | ||
| Line 17: | Line 14: | ||
* In terms of the [[Marginal Default Probability]] we have <math>p_k = h_k / (1 - q_{k-1}) </math> where <math>h_k</math> is the marginal default probability during period <math>[t_{k-1}, t_k]</math>. The marginal default probability is also denoted the [[Hazard Rate]] | * In terms of the [[Marginal Default Probability]] we have <math>p_k = h_k / (1 - q_{k-1}) </math> where <math>h_k</math> is the marginal default probability during period <math>[t_{k-1}, t_k]</math>. The marginal default probability is also denoted the [[Hazard Rate]] | ||
* In terms of the [[Survival Probability]] we have <math>p_k = S_{k-1} - S_k </math> where <math>S_k</math> is the survival probability up to point <math>t_k</math> | * In terms of the [[Survival Probability]] we have <math>p_k = S_{k-1} - S_k </math> where <math>S_k</math> is the survival probability up to point <math>t_k</math> | ||
| + | |||
| + | == Issues and Challenges == | ||
| + | * It is important to distinguish the incremental default probability from the [[Marginal Default Probability]] which is conditional on no default prior to the current period.''' | ||
| + | |||
---- | ---- | ||
[[Category:Credit Curve]] | [[Category:Credit Curve]] | ||
[[Category:Credit Network]] | [[Category:Credit Network]] | ||
Revision as of 11:28, 31 March 2021
Definition
The term Incremental Default Probability is used in the context of multi-period credit risk analysis to denote the likelihood that a legal entity is observed to have experienced a Credit Event during a defined period of time.
The incremental default probability can be considered as another building block of the Credit Curve, alternative to the Cumulative Default Probability representation.
Notation
Observing whether an entity is defaulted over a period ![[t_{k-1}, t_k]](https://www.openriskmanual.org/wiki/images/mathdata/5/f/c/5fca5d2a31e321534bcf5a74a56b3db1.png) , the incremental default probability is denoted
, the incremental default probability is denoted 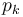 . Incremental default probabilities} during period k, given an initial rating of m, are denoted by
. Incremental default probabilities} during period k, given an initial rating of m, are denoted by
- In terms of the Cumulative Default Probability we have
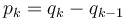 where we denote with
where we denote with 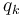 the cumulative default probability up to time
the cumulative default probability up to time 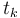
- In terms of the Marginal Default Probability we have
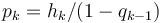 where
where 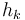 is the marginal default probability during period
is the marginal default probability during period ![[t_{k-1}, t_k]](https://www.openriskmanual.org/wiki/images/mathdata/5/f/c/5fca5d2a31e321534bcf5a74a56b3db1.png) . The marginal default probability is also denoted the Hazard Rate
. The marginal default probability is also denoted the Hazard Rate - In terms of the Survival Probability we have
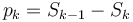 where
where 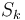 is the survival probability up to point
is the survival probability up to point 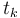
Issues and Challenges
- It is important to distinguish the incremental default probability from the Marginal Default Probability which is conditional on no default prior to the current period.
![\mbox{PD}^{m}_{t,k} = p^m_k = 1_E [ 1_{\{ R_{k} = D \}} | F_t, R_0=m] = P(R_k=D | F_t, R_0=m)](https://www.openriskmanual.org/wiki/images/mathdata/b/8/8/b88fda1e52221cafe1b238378dfcaf1e.png)