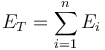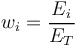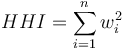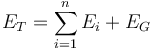Herfindahl-Hirschman Index
Contents
Definition
For the purpose of measuring credit portfolio or market Concentration Risk (e.g., name, sector or geographic risk), diversity or inequality metrics, the Herfindahl-Hirschman Index (HHI) is defined as the sum of all squared relative portfolio shares of the exposures.
Details
More precisely, if we have n exposures 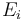 summing up to a total exposure of
summing up to a total exposure of
and each exposure fraction is defined as
Then the HHI index is defined as
Assuming the exposure data are given, it is easy to calculate the HHI by first forming the fractional (normalized) exposures and then computing and summing up their squares. By construction, the HHI is restricted between zero and one, with one corresponding to full concentration to one counterparty. Sometimes the inverse of the index is also used.
Usage
Interpretation and Concentration levels
Whether a given result indicates a concentrated portfolio cannot be assessed beforehand but only in relation with typical portfolios, standard market practices etc. or other metrics. Concentration levels can characterized as no, low or medium to high to "total" concentration based on subjective thresholds.
For example in the context of corporate sector market share analysis an HHI below 0.15 is deemed "not concentrated," between 0.15 is 0.25 as "moderately concentrated," and above 0.25 as highly concentrated (monopolistic / oligopolistic). These thresholds might not be appropriate to use in the context for financial risk concentrations
Connection with risk based measures
In a risk based framework for concentration management, the HHI is linked to portfolio volatility
Advantages
Key advantages of the HHI index include
- Computational simplicity
- Relatively moderate data requirements (but see qualification below)
- Unambiguous definition: Compared to the simpler Concentration Ratio measures the HHI index does not require specifying which fraction of the portfolio to focus
Disadvantages
The difficulty to interpret the index on an absolute basis is already mentioned. The HHI can be misleading as a risk measure because of several further limitations:
- It does not consider the borrower's credit quality. An exposure to a Aaa-rated borrower, for example, is treated in the same way as an exposure to a B-rated borrower.
- It does not account for credit risk dependencies between borrowers. Two large exposures to borrowers belonging to the same supply chain and located in the same town are treated in the same way as two large exposures to borrowers in completely unrelated industry sectors and located on different continents.
- It does not account for the nature of the exposure. A long dated exposure in a derivatives portfolio can lead to substantial mark-to-market losses if the counterparty deteriorates, even if there is no default event
- It does no enable to express a risk appetite statement around concentration. There is no obvious implied stress level linked to a particular HHI value.
Variations
The HHI index has been independently discovered and used in various fields with other names and / or simple transformations. The following are all alternative names
- Gibbs–Martin index
- Blau index
- Gini–Simpson index
The following transformations of the HHI are in common use
- Square root
- Inverse
- Unit Complement (1 -HHI)
Calculation in presence of granular exposures
When the exposure data contain a large amount of very small exposures it may be acceptable and computationally advantageous to compute the index assuming the small exposures do not contribute to concentration. This is done simply by adding a total granular exposure 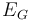 so that
so that
Hence while small exposures are added and increase the total exposure, they are assumed by construction to have zero contribution to the HHI summation
Issues and Challenges
- The first limitation can be addressed by a rating-weighted HHI. The squared relative exposure shares are weighted in the aggregation by a numeric borrower rating, thereby giving more weight to borrowers with a lower credit quality. See also the link of HHI with risk based measures below.
- The second limitation, the ignorance of default dependencies, cannot be remedied in a similarly simple way. As a rating- weighted HHI provides a ranking in terms of name concentration, it can be useful for a comparison across credit portfolios; yet, it fails to produce a capital figure for low granularity
Implementations
Open Source implementations of the Herfindahl-Hirschman index are available in
- the R package Ineq
- the Python library Concentration Library
- Spreadsheet Implementation
Implementation Challenges
Although the data requirements for the HHI calculation seem to be moderate at first sight, they often turn out to be difficult to meet in practice. They require nothing less than the aggregation of all exposures to the same borrower for the whole business entity, be it a bank or a banking group. A heterogeneous IT environment can already present a serious technical obstacle to this aggregation. Furthermore, large borrowers, which are actually the most relevant entities for measuring name concentration, can themselves be complex structures that are not always easy to identify as belonging to the same borrower entity.
See Also
None