Difference between revisions of "Dynamic Input-Output Models"
Wiki admin (talk | contribs) |
Wiki admin (talk | contribs) (→Formula) |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
| − | '''Dynamic Input-Output Models''' is a category of various possible generalization of the basic [[Input-Output Model]] that allow accounting for more sophisticated temporal behavior<ref>Eurostat Manual of Supply, Use and Input-Output Tables, 2008 edition</ref> | + | '''Dynamic Input-Output Models''' is a category of various possible generalization of the basic [[Input-Output Model]] that allow accounting for more sophisticated temporal behavior <ref>Eurostat Manual of Supply, Use and Input-Output Tables, 2008 edition</ref>, <ref>R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009</ref> |
| + | |||
| + | Dynamic (inter-temporal) frameworks can address phenomena such as stock accumulation (both physical and capital), technology changes and other time-dependent developments that cannot be represented in a stationary equilibrium model. | ||
| + | |||
| + | Mathematically the equations of the standard IO model become finite difference equations relating two or more timepoints. | ||
== Formula == | == Formula == | ||
| − | + | Typical equations of a dynamic input-output model are: | |
| − | * | + | * <math>X_t = A X_t + C_t + D_t</math> |
| − | * | + | * <math>D_t = B (X_{t+1} - X_{t})</math> |
| − | * | + | * <math>X_t = A X_t + C_t + B (X_{t+1} - X_{t})</math> |
| − | * (I | + | * <math>(I - A + B) X_t = C_t + B X_{t+1}</math> |
| − | The production of period t is | + | The total production vector X of period t is related to the production in period t+1 through equation: |
| − | |||
| + | :<math> | ||
| + | X_t = (I - A + B)^{-1} (C_t + B X_{t+1} ) | ||
| + | </math> | ||
| − | while the production of period t+1 is | + | while the production of period t+1 is related to the production in period t through the inverse equation: |
| − | |||
| + | :<math> | ||
| + | X_{t+1} = B^{-1}[(I - A + B) X_t - C_t] | ||
| + | </math> | ||
Where: | Where: | ||
| − | * Y | + | * Y is the [[Final Demand]] which splits into C + D, where in turn |
| − | * I | + | ** C is the exogenous final demand (consumption) |
| − | * A | + | ** D is the induced investment |
| − | * (I-A)-1 | + | * B are the input coefficients for capital (the amount of sector i product (in dollars) held as capital stock for production of one dollar’s worth of output by sector j). |
| − | * | + | * I is the unit (identity) matrix |
| − | + | * A are input coefficients for intermediate production ([[Technical Coefficient Matrix]]) | |
| − | + | * <math>(I - A)^{-1}</math> is the matrix of cumulative input coefficients ([[Leontief Inverse Matrix]]) | |
| − | + | * t is the time index of successive periods | |
| + | |||
| + | This is a system of linear difference equations, since the values of the variables X are related to different periods of time. NB: In this example the coefficient matrices are assumed time invariant. | ||
| − | + | If B is zero (no amounts held in capital stock), the equations reduce to the standard (stationary) model. | |
== Issues and Challenges == | == Issues and Challenges == | ||
| − | Practical problems relate to the matrix B of capital coefficients. | + | * Practical problems relate to the matrix B of capital coefficients. Only a few sectors produce capital goods. Therefore it can not be expected that matrix B has an inverse. There is a large literature on the singularity problem in the dynamic input-output model and many problems remain for empirical applications. |
| + | |||
| + | == Further Resources == | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=70 Crash Course on Input-Output Model Mathematics] | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=64 Introduction to Input-Output Models using Python] | ||
== References == | == References == | ||
Latest revision as of 16:39, 16 November 2023
Definition
Dynamic Input-Output Models is a category of various possible generalization of the basic Input-Output Model that allow accounting for more sophisticated temporal behavior [1], [2]
Dynamic (inter-temporal) frameworks can address phenomena such as stock accumulation (both physical and capital), technology changes and other time-dependent developments that cannot be represented in a stationary equilibrium model.
Mathematically the equations of the standard IO model become finite difference equations relating two or more timepoints.
Formula
Typical equations of a dynamic input-output model are:
The total production vector X of period t is related to the production in period t+1 through equation:
while the production of period t+1 is related to the production in period t through the inverse equation:
Where:
- Y is the Final Demand which splits into C + D, where in turn
- C is the exogenous final demand (consumption)
- D is the induced investment
- B are the input coefficients for capital (the amount of sector i product (in dollars) held as capital stock for production of one dollar’s worth of output by sector j).
- I is the unit (identity) matrix
- A are input coefficients for intermediate production (Technical Coefficient Matrix)
-
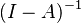 is the matrix of cumulative input coefficients (Leontief Inverse Matrix)
is the matrix of cumulative input coefficients (Leontief Inverse Matrix) - t is the time index of successive periods
This is a system of linear difference equations, since the values of the variables X are related to different periods of time. NB: In this example the coefficient matrices are assumed time invariant.
If B is zero (no amounts held in capital stock), the equations reduce to the standard (stationary) model.
Issues and Challenges
- Practical problems relate to the matrix B of capital coefficients. Only a few sectors produce capital goods. Therefore it can not be expected that matrix B has an inverse. There is a large literature on the singularity problem in the dynamic input-output model and many problems remain for empirical applications.
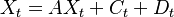
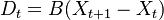
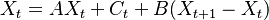
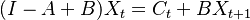
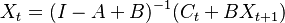
![X_{t+1} = B^{-1}[(I - A + B) X_t - C_t]](https://www.openriskmanual.org/wiki/images/mathdata/5/6/a/56a91fc98a639bf79666c56d0ec49505.png)