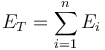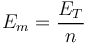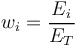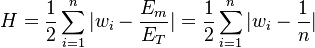Hoover Index

Definition

For the purpose of measuring name, sector or geographic concentration, the Hoover Index is a simple index defined in terms of the absolute deviation from the mean (The 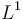$L^1$ norm).

Details

More precisely, if we have n exposures 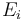$E_i$ summing up to a total exposure of

$E_T = \sum^{n}_{i=1} E_{i}$

an average exposure

$E_m = \frac{E_T}{n}$

and fractional exposures 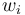$w_i$ are defined as

$w_{i} = \frac{E_i}{E_T}$

Then the Hoover index is defined as

$H = \frac{1}{2} \sum^{n}_{i=1} | w_i - \frac{E_m}{E_T} | = \frac{1}{2} \sum^{n}_{i=1} | w_i - \frac{1}{n} |$

Usage

None

Variations

None

Issues and Challenges

None

Implementation

Open Source implementations of the Hoover index are available in

• the Python library Concentration Library

See Also

None