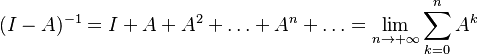Power Series Approximation
From Open Risk Manual
Definition
Power Series Approximation in the context of IO analysis is the representation of a Leontief Inverse Matrix as an infinite sum of powers of the Technical Coefficient Matrix. [1] In mathematical terminology this is known as the Neumann Power Series.
Formula
The power series converges only under certain conditions:
-
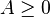 (the coefficients matrix contains only non-negative terms)
(the coefficients matrix contains only non-negative terms) - The system produces more output than it requires inputs
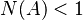
- The Leontief matrix is non-singular,
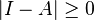
- More generally, the Hawkins-Simon conditions apply
Usage
The power series approximation makes it more explicit that the Leontief inverse matrix represents value chain interrelations at an ever increasing expansion of the interacting entities required to produce an output.
Issues and Challenges
- For large matrices there may be significant computational power or specialized software required to evaluate the expansion
Further Resources
References
- ↑ R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009