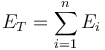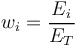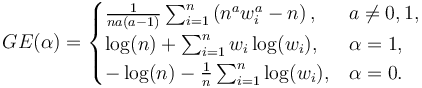Generalized Entropy Index
From Open Risk Manual
Contents
Definition
For the purpose of measuring concentration, the Generalized Entropy Index is measure of concentration that draws from concepts of information theory
Details
If the total exposure is
and the fractional exposures 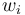 are defined as
are defined as
Then the Generalized Entropy index is defined as
Relation with the Theil Index
The Theil Index is the Generalized Entropy Index for a = 1
Usage
None
Variations
None
Issues and Challenges
None
Implementations
Open Source implementations of the Generalized Entropy index are available in
- the R package Ineq
- the Python library Concentration Library