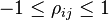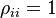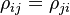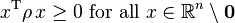Correlation Matrix
Contents
Definition
A Correlation Matrix denotes both a measure and a statistical of dependency (whether causal or not) between different stochastic processes
NB: This article focuses on aspects of correlation matrices relevant for risk management applications. More general statistical considerations are available in the wikipedia entry and links therein
Alternative Correlation Measures
There are several alternative measures of correlation:
- The Pearson Correlation also referred to as Pearson's r, the Pearson product-moment correlation coefficient or the bivariate correlation, a measure of the linear correlation between two variables X and Y
- The Spearman's Rank Correlation a nonparametric measure of rank correlation (statistical dependence between the rankings of two variables)
- The Kendall Rank Correlation as Kendall's tau coefficient a statistic used to measure the ordinal association between two variables
Properties
Valid Range
All correlation matrix elements must satisfy
The diagonal elements must be identical to unity
Symmetry
The matrix elements must satisfy the symmetry relation
Positive Semi-Definiteness
A correlation matrix must be positive semi-definite, namely
When a matrix fails this requirement (usually due to Data Quality issues) one usually aims to find a nearby matrix that is valid. One approach to fix an invalid correlation matrix is provided here[1]
An equivalent requirement is that all eigenvalues of the matrix are non-negative (See Definiteness of a matrix)
Characterization
Correlation matrices are in general characterised according to the distribution of eigenvalues
See Also
References
- ↑ Higham, Nick (2002) Computing the nearest correlation matrix - a problem from finance; IMA Journal of Numerical Analysis 22