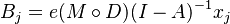Biodiversity Loss
Contents
Definition
Biodiversity Loss is the reduction in number of Species due to anthropogenic factors. It is the worldwide extinction of different species, as well as the local reduction or loss of species in a certain habitat, resulting in a loss (reduction) of biological diversity.
The reduction of any aspect of biological diversity (i.e., diversity at the genetic, species and ecosystem levels) is lost in a particular area through death (including extinction), destruction or manual removal; it can refer to many scales, from global extinctions to population extinctions, resulting in decreased total diversity at the same scale.
EEIO Approach to Biodiversity Loss
The impact of human economic activity on biodiversity loss can be approximated via an Environmental Input-Output Model[1], [2].
- The first step is the combination of company or portfolio data with the MRIO model to translate into production and purchases per industry and region, in order to assess the impact of the whole upstream value chain
- The second step gives information on the contributions of the activity to the drivers of biodiversity loss (e.g., emission of GHGs and consumption of raw materials and water). This is calculated based on the environmental extensions of the EEMRIO model.
- The third step gives information on the loss of biodiversity caused per unit of driver (e.g., kg CO 2-eq, ton of raw material)
Formula
In the context of an EEIO model constructed with suitable economic and ecological data if t is the number of environmental pressures considered, r is the number of regions in the IO model, and s is the number of industries in the IO model the biodiversity loss is computed as:
where:
- impact
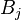 is the biodiversity footprint of sector j
is the biodiversity footprint of sector j - e is a (1 times t) vector of ones used to sum up the biodiversity losses caused by an individual environmental pressure
- M is the (t times r.s) matrix of biodiversity loss factors;
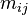 is a (1 times s) row vector of biodiversity loss factors of direct environmental pressure i in region j (depicting the biodiversity losses per unit of environmental pressure)
is a (1 times s) row vector of biodiversity loss factors of direct environmental pressure i in region j (depicting the biodiversity losses per unit of environmental pressure) - D is the (t times r.s) matrix of direct environmental pressures;
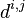 is a (1 times s) row vector of direct environmental pressure intensities of pressure i in region j depicting the direct environmental pressures of one unit of production for all sectors
is a (1 times s) row vector of direct environmental pressure intensities of pressure i in region j depicting the direct environmental pressures of one unit of production for all sectors - I is the identity matrix (with dimension r·s times r·s)
-
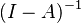 is the Leontief Inverse Matrix (also with dimension r·s times r·s)
is the Leontief Inverse Matrix (also with dimension r·s times r·s) - x is a (r.s times 1) vector of production with zeros for all sectors except sector j (NB hence not the usual Final Demand vector)
- The binary operation
 is the element-wise multiplication of two matrices (the Hadamard product)
is the element-wise multiplication of two matrices (the Hadamard product)
Issues and Challenges
- Indirect quantification of biodiversity loss that may be missing critical channels and mechanisms
- Overall a linear approach that does not take into account dependencies in ecological systems