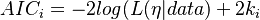Akaike Information Criterion
Contents
Definition
The Akaike Information Criterion (AIC) was introduced by Hirotsugu Akaike in his seminal 1973 paper, "Information theory and an extension of the maximum likelihood principle". Akaike extended the traditional Maximum Likelihood paradigm by considering a framework in which the model dimension is also unknown and must, therefore, be determined from the data. Thus Akaike proposed a framework in which both model estimation and model selection can be simultaneously accomplished.[1]
Formula
The general expression for the AIC is:
where 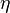 is the maximum likelihood estimation of model parameters, k is the number of parameters,
is the maximum likelihood estimation of model parameters, k is the number of parameters, 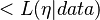 is the likelihood of the function, log is the natural logarithm, and i is the i model (or PI) for which the AIC is computed.
is the likelihood of the function, log is the natural logarithm, and i is the i model (or PI) for which the AIC is computed.
The corrected version of the AIC, AICc, is usually adopted in applications in which the number of parameters, k, is large relative to sample size
Usage
The use of the AIC (or AICc) requires knowing the log-likelihood associated with any candidate model, which in turn requires application of a maximum likelihood estimation (MLE) procedure. In order to use an MLE, one has to assume the type of underlying distribution in order for the appropriate likelihood function to be derived and the parameters estimated.
See Also
References
- ↑ Operational risk – Revisions to the simpler approaches, BIS 2014