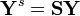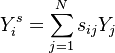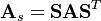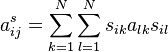Aggregation Matrix
Contents
Definition
Aggregation Matrix (also Summation Matrix) in the context of Input-Output Analysis is a Boolean Matrix that aims to produce a coarse-grained version of a more granular Input-Output Model.
Aggregation can be for example along sectoral or regional dimensions.
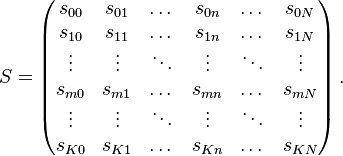
Vectors and Matrices can be aggregated by multiplying with the aggregation matrix. Mathematically a aggregation matrix S is a 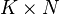 matrix, where each value
matrix, where each value 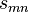 is either zero or one. The aggregation matrix has in total N non-zero values.
is either zero or one. The aggregation matrix has in total N non-zero values.
An aggregation matrix with K rows and N columns is used to aggregate a dimension of size N into a smaller dimension of size K. The N non-zero (unit) values select and group the elements of the vector or matrix that is to be aggregated.
Vector Quantity Aggregation
A vector Y of dimension N is aggregated into a vector K through its pre-multiplication with the aggregation matrix.
or more explicitly:
Matrix Quantity Aggregation
A matrix of dimension N x N is aggregated into a K x K matrix through its pre-multiplication with the aggregation K x N matrix and the post-multiplication with the (N x K) aggregation matrix transpose.
or more explicitly: