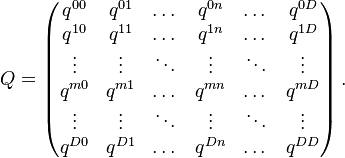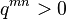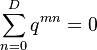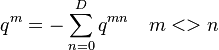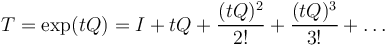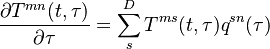Transition Rate Matrix

Definition

A Transition Rate Matrix, also, known as the "Infinitesimal Generator" of a Transition Matrix is a square (n x n) matrix representing the transition rates of a multi-state stochastic system (e.g. a Markov Chain). It measures the probability (per unit of time) that an event (state transition) occurs within an infinitesimally small time interval.

The size n of the matrix is linked to the cardinality of the State Space that describes the system being modelled. Lets assume a state space 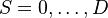$S ={0, \dots ,D}$. If the rate of moving from state m to state n in an infinititesimal time period is 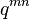$q^{mn}$, the transition rate matrix 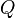$Q$ is given by using 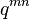$q^{mn}$ as the 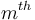$m^{th}$ row and 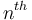$n^{th}$ column element:

$Q=\left(\begin{matrix} q^{00} & q^{01} & \dots &q^{0n} & \dots & q^{0D} \\ q^{10} & q^{11} & \dots &q^{1n} & \dots & q^{1D} \\ \vdots & \vdots & \ddots &\vdots & \ddots & \vdots \\ q^{m0} & q^{m1} & \dots &q^{mn} & \dots & q^{mD} \\ \vdots & \vdots & \ddots & \vdots& \ddots & \vdots \\ q^{D0} & q^{D1} & \dots & q^{Dn} & \dots & q^{DD}\\ \end{matrix}\right).$

Properties

• Since the transition rates are refer to the probabilities of transitions they must be positive (but need not be less than unity)

$q^{mn} > 0$

• Since a system must migrate to any of the available states (inclusive of possibly staying in the same state) the transition rate matrix must satisfy:

$\sum_{n=0}^D q^{mn}= 0\,$

Equivalently to the summation property, the diagonal elements are by convention denote as

$q^{m} = - \sum_{n=0}^D q^{mn} \quad m <> n$

Generating a Transition Matrix

A transition rate matrix Q gives rise to a transition matrix T via:

$T = \exp(t Q) = I + t Q + \frac{(t Q)^2}{2!} + \frac{(t Q)^3}{3!} + \dots$

Chapman-Kolmogorov Equation

In differential form, the evolution of transition probabilities as a function of the transition rates is given by the forward Chapman-Kolmogorov Equation:

$\frac{\partial T^{mn}(t, \tau)}{\partial \tau} = \sum_s^{D} T^{ms}(t, \tau) q^{sn}(\tau)$

Characterization

Transition rate matrices can vary significantly in the type of transition phenomena they capture. Some variations can be captured in well defined mathematical conditions satisfied by the matrix elements

Time Homogeneity

When the transition rates do not depend on time 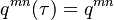$q^{mn}(\tau) = q^{mn}$ we have the simpler category of time homogeneous transition phenomena (which also significantly simplifies calculations)

Estimation

The empirical estimation of a transition rate matrix is via the Aalen-Johansen Estimator

---