Risk Measure
From Open Risk Manual
Contents
Definition
A Risk Measure is a type of Risk Metric derived from a Risk Distribution (a representation of risk in terms of a Random Variable).
More formally, let 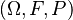 be a probability space and
be a probability space and 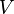 be a non-empty set of F-measurable real-valued random variables. Then any mapping
be a non-empty set of F-measurable real-valued random variables. Then any mapping 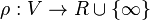 is called a risk measure.
is called a risk measure.
Types of Risk Measures
There are several distinct types of risk measures:
- Statistical Moments, e.g. the variance
- Quantile measures (e.g. Value at Risk)
- Coherent Risk Measure (e.g. Expected Shortfall)
- Concentration Indexes
Desirable characteristics of risk measures
An ideal risk measure should be intuitive, stable, easy to compute, easy to understand, coherent and interpretable in economic terms. Additionally, risk decomposition based on the risk measure should be simple and meaningful [1]
- Intuitive: The risk measure should meaningfully align with some intuitive notion of risk, such as unexpected losses.
- Stable: Small changes in model parameters should not produce large changes in the estimated loss distribution and the risk measure. Similarly, another run of a simulation model in order to generate a loss distribution should not produce a dramatic change in the risk measure. Also, it is desirable for the risk measure not to be overly sensitive to modest changes in underlying model assumptions.
- Easy to compute: The calculation of the risk measure should be as easy as possible. In particular, the selection of more complex risk measures should be supported by evidence that the incremental gain in accuracy outweighs the cost of the additional complexity.
- Easy to understand: The risk measure should be easily understood by the bank’s senior management. There should be a link to other well-known risk measures that influence the risk management of a bank. If not understood by senior management, the risk measure will most likely not have much impact on daily risk management and business decisions, which would limit its appropriateness
- Coherent: The risk measure should be coherent and satisfy the conditions of:
- monotonicity (if a portfolio Y is always worth at least as much as X in all scenarios, then Y cannot be riskier than X)
- positive homogeneity (if all exposures in a portfolio are multiplied by the same factor, the risk measure also multiplies by that factor)
- translation invariance (if a fixed, risk-free asset is added to a portfolio, the risk measure decreases to reflect the reduction in risk) and
- subadditivity (the risk measure of two portfolios, if combined, is always smaller or equal to the sum of the risk measures of the two individual portfolios). This property that a risk measure appropriately accounts for diversification.
- Simple and meaningful risk decomposition (risk contributions or capital allocation): In order to be useful for daily risk management, the risk measured for the entire portfolio must be able to be decomposed to smaller units (eg business lines or individual exposures). If the loss distribution incorporates diversification effects, these effects should be meaningfully distributed to the individual business lines
References
- ↑ BCBS, Range of practices and issues in economic capital frameworks. 2009