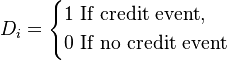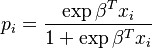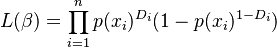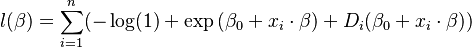Logistic Regression Credit Scorecard
Contents
Definition
Credit Scorecards based on Logistic Regression are a type of credit scoring model in widespread use to support Credit Decisioning in various Consumer Finance and SME Lending businesses.
This entry serves as the Abstract Risk Model specification of a Logistic Regression Scorecard
Model Context
A population of borrowers characterised by individual features (characteristics, attributes) associated with each obligor and assumed to represent credit score factors, that is, indicators of propensity to default. The population is modelled statistically for the likelihood for defaulting (or not) over a defined period of time (the Risk Horizon).
Model Classification
The model belongs to the following categories
- discriminative (the population characteristics are not modelled)
- parametric (a set of weights represents the parameters of the model)
- exclusively observed variables
- non-linear (generalized linear)
- supervised (the historical default behaviour represents the label)
- elementary algorithm (represented by the logit model class
- frequentist approach (most commonly estimated directly on historical datasets)
Model Description
Response Variable
In binary or dichotomous logistic regression the response variable 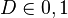 follows a Bernulli distribution. The response variable
follows a Bernulli distribution. The response variable 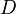 captures the realization or not of a Credit Event involving the i-th borrower:
captures the realization or not of a Credit Event involving the i-th borrower:
Explanatory Variables
The Explanatory Variables form an n dimensional vector 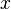 that comprises potentially of both continuous and discrete (categorical) variables
that comprises potentially of both continuous and discrete (categorical) variables
Model Parameters
A n+1 dimensional vector 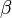 (including the offset as the zero-th element) of parameters to be estimated
(including the offset as the zero-th element) of parameters to be estimated
The Functional Form
Model Estimation
Estimation is via Maximum Likelihood. Given a vector of realized outcomes 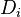 the likelihood function L is:
the likelihood function L is:
The log-likelihood is
Stylized Model Assumptions
- The observations of the response variable
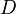 are independent from each other. This assumption is manifestly not true as it is well established the defaults are correlated (Default Dependency)
are independent from each other. This assumption is manifestly not true as it is well established the defaults are correlated (Default Dependency) - The explanatory variables combine in a linear fashion
- The specific logistic functional form is ad-hoc and does not have any economic interpretation