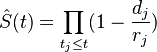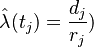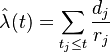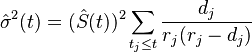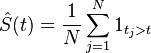Kaplan-Meier Estimator

Definition

The Kaplan-Meier estimator is a nonparametric estimator of the Survival Function from (possibly censored) data. It concerns the special case when the State Space of the stochastic system has only two states (Alive / Dead) and one of them is an absorbing state, that is, once the system reaches this state it never leaves.

Estimator

The position in state space for an entity 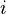$i$ in continuous time 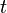$t$ is a Random Variable 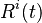$R^i(t)$ taking values in the state space S (We assume a finite state space 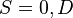$S ={0, D}$), where 0 is the live (healthy / performing) state and D is the dead (non-performing) state.

Denote 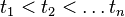$t_1 < t_2 < \dots t_n$ the times at which entities transition from state 0 to state D and let 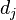$d_j$ the cumulative count of such transitions at time 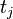$t_j$. Then the estimator is given by the expression:

$\hat{S}(t) = \prod_{t_j \le t} (1 - \frac{d_j}{r_j})$

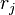where $r_j$ is the number of entities that are alive prior to time $t_j$.

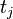The Kaplan-Meier hazard rate estimator is simply

$\hat{\lambda}(t_j) = \frac{d_j}{r_j})$

The Nelson-Aalen estimator for the cumulative hazard is

$\hat{\lambda}(t) = \sum_{t_j \le t} \frac{d_j}{r_j}$

Variance

The variance of the Kaplan-Meier estimator is given by Greenwood's formula:

$\hat{\sigma}^2(t) = (\hat{S}(t))^2 \sum_{t_j \le t} \frac{d_j}{r_j (r_j - d_j)}$

No Censoring

In the case of no censoring, the Kaplan-Meier estimator is equivalent to the empirical survival function. If the population involves N entities, this is given by:

$\hat{S}(t) = \frac{1}{N} \sum_{j=1}^{N} 1_{t_j > t}$

See Also

• Cohort Estimator
• Aalen-Johansen Estimator