How to Generate Correlated Random Numbers
Contents
Generation of correlated random numbers is of wide applicability in many domains of quantitative analysis and risk modelling. This article is a review of approaches.
Precise Problem Definition
The more precisely defined question is how to generate random numbers 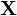 according to a defined multivariate probability distribution.
according to a defined multivariate probability distribution.
Special Cases
The most commonly encountered special case is that of multivariate normal distribution given by the density:
For the purposes of this article will ignore non-zero means and non-unit (unscaled) variances as those aspects can be handled on a univariate basis. We will focus on the Correlation Matrix.
In general the methodologies involve generating realizations of the random (vector) 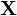 on the basis of a random vector
on the basis of a random vector 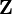 of uncorrelated normal variables, which in turn are (typically) produced by a random vector
of uncorrelated normal variables, which in turn are (typically) produced by a random vector 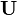 of uncorrelated uniform variables.
of uncorrelated uniform variables.
Cholesky Decomposition
Given the variance-covariance matrix 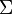 (that is positive definite), the Cholesky decomposition is
(that is positive definite), the Cholesky decomposition is
Upon simulation of random vectors 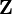 the correlated realisations are provided by:
the correlated realisations are provided by:
where L is a lower triangular matrix that is effectively the "square-root" of the correlation matrix
Singular Value Decomposition
When the correlation matrix is estimated empirically it may be the case that it fails to be positive semi-definite, in which case the Cholesky decomposition may fail. One option is to adjust the correlation matrix. Another option is to pursue a singular value decomposition
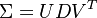 , where U, V are orthogonal matrices and D is diagonal (with possibly reduced rank, ie. some eigenvalues are zero).
, where U, V are orthogonal matrices and D is diagonal (with possibly reduced rank, ie. some eigenvalues are zero).
Then
Prespecified Linear Models
It is not always the case that our input data or modelling framework is based on covariance matrix. If the dependency between dependent variables is explicitly derived in terms of a multi-factor model wher the factors 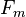 are uncorrelated then the problem is reduced to generating independent random numbers and subsequently constructing suitable sums:
are uncorrelated then the problem is reduced to generating independent random numbers and subsequently constructing suitable sums:
The simplest example being the case
Box–Muller transform
The wikipedia:Box–Muller transform is an interesting special case, primarily of interest for educational purposes. In the first step uncorrelated normal numbers are generated via
Those can then be combined as per the formulas of the previous section on linear models
Copulas
In various applications the multi-variate dependency cannot be assumed to be a Gaussian. In this case we require to have a specified copula which provides for more general dependency structures.
The copula of 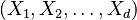 is defined as the cumulative distribution function of
is defined as the cumulative distribution function of 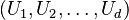 via
via
The Student-t Copula
This is a special copula as it is linked to the Gaussian distribution
Archimedean Copulas
- Clayton
- Gumbel
- Frank
Empirical Copula
Applications
Implementation
A list of open source implementations
| Library / Package | Language | Characteristics |
|---|---|---|
| XXX | Python | TD |
| XXX | R | TD |
| XXX | C++ | TD |
| XXX | Julia | TD |
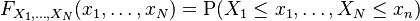
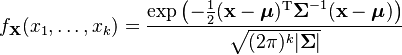
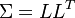
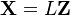
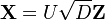
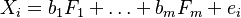
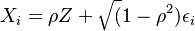
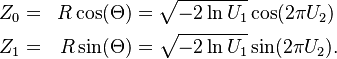
![C(u_1,u_2,\dots,u_d)=\mathrm{Pr}[U_1\leq u_1,U_2\leq u_2,\dots,U_d\leq u_d] .](https://www.openriskmanual.org/wiki/images/mathdata/0/5/6/05656bc8a1525e98116cca0dc116f194.png)