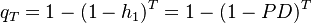How to Estimate Lifetime PD from 12 month PD

How to Estimate Lifetime PD from 12 month PD

This is a frequent question in the context of estimating Lifetime PD for example when developing an IFRS 9 or CECL reporting framework.

Why is the question relevant

The question arises typically because the institution interested in the lifetime [Probability of Default]] estimate has already in place a methodology or tools for estimating an annual probability of default. This will typically be the case where such an estimate is used for Regulatory Capital purposes. Re-using estimates or data / models would thus both be efficient and potentially more consistent

Strict estimation is not possible

Conceptually the likelihood of default over a long period of time is correlated with the likelihood of default over a shorted period of time but the precise relation is not known and may vary significantly. An estimate of lifetime PD starting with a 12 month PD will thus necessarily involve additional Model Assumptions which may or may not be realistic or suitable for the application at hand

Assuming a flat term structure

A common simplifying assumption is that the Hazard Rate (Credit Curve) of the credit risk process has a flat Term Structure, which means that the Marginal Default Probability on any given future year (conditional on survival) is the same as the first year. Under this assumption, if we denote this marginal default probability as 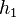$h_1$ and set it equal to the first year PD ($p_1$)

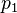The general expression of the Cumulative Default Probability is 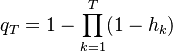$q_T = 1 - \prod_{k=1}^{T} (1 - h_k)$. Given the constant hazard rate assumption this reduces to:

$q_T = 1 - (1 - h_1)^{T} = 1 - (1 - PD)^{T}$

The meaning of this expression is easier to grasp if we consider the multi-year Survival Probability which is just the product of the one year survival probabilities (1 - PD)

Suitability

The suitability of the flat term structure assumption cannot be established a-priori and depends on the entity or entities being modeled. There are example where the assumption is conservative and vice-versa. For example some pools of retail credit are known to exhibit Seasoning, that is the future likelihood of default diminishes the longer the survival period. On the other hand highly rated corporate entities are known to have increased default risk over time.

Adjustments

It is conceivable that some data or expert knowledge is available to validate the flat term structure assumption. In that case it may be possible to produce a suitable estimate by using e.g. slopping hazard rate curve

Other considerations

As discussed in more detail in the IFRS 9 versus IRB Models entry, beyond the purely mathematical considerations, re-using a probability of default that has been developed for regulatory purpose may raise other issues (Default Definition, Margin of Conservatism)

---