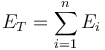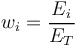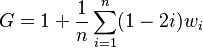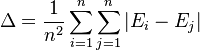Gini Index
From Open Risk Manual
Contents
Definition
For the purpose of measuring concentration, the Gini Index (also Gini coefficient) is an index defined in terms of the Lorentz curve of distribution values.
Details
More precisely, if we have n values 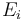 summing up to a total value of
summing up to a total value of
and the fractional value 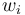 is defined as
is defined as
Then the Gini index is defined as the area under the Lorenz curve which is geometrically reduced to
Alternative Formula
Gini's absolute mean difference is defined as
The relative mean difference is defined as 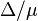 where
where 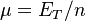
The Gini index is equivalently given by
Usage
None
Variations
None
Issues and Challenges
NB: Sometimes the formula appears also with the opposite sign!
Implementations
Open Source implementations of the Gini index are available in
- the R package Ineq
- the Python library Concentration Library