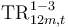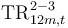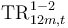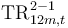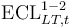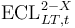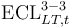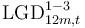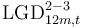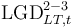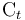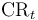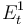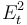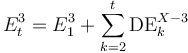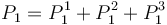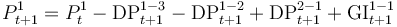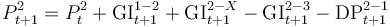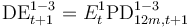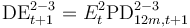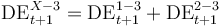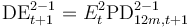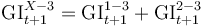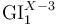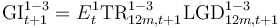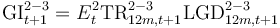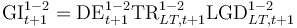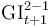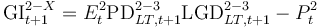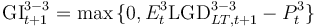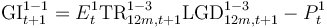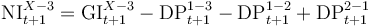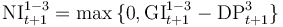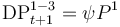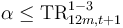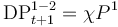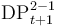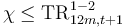EBA 2018 Stress Test Definitions
This set of definitions are part of the EBA 2018 Stress Test Methodology of the upcoming EBA 2018 EU-Wide Stress Test
The bold face numerals refer to the defining paragraph at the Methodology Document
Risk Parameters and Other Variables
Risk Parameters are defined first, to enable expressing subsequent definitions in terms of these. Parameters are the forward-looking projections of 12-month transitions between each of the three stages and the associated loss rates.
- Transition rates (TR) denote the probability of moving between the stages (S1, S2 or S3) within 12 months.
- LGD refers to forecasted losses associated with possible S3 events.
- Subscripts denote the event horizon where 12M refers to S3 events possible within 12 months.
- For the lifetime horizon (denoted by a subscript LT), loss rates (LR) have to be reported which refer to the expected credit losses due to stage 3 events expected over the lifetime of the exposures. For example, the total exposure in S2 multiplied by LRLT2-X should give the lifetime expected credit losses required. This means there is no requirement to separately project lifetime transitions to S3 for S2 exposures.
- Superscripts indicate the applicable transition in that year (e.g. 1-3 indicates that the parameter refers to S1 to S3 transitions in year t
| Term |
Formula |
Definition / Notes
|
| S1 PD |
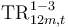 |
76.a Refers to the probability of an exposure starting the year in S1 and ending in S3
|
| S2 PD |
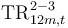 |
76.b Refers to the probability of an exposure starting the year in S2 and ending in S3
|
| SICR Rate |
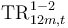 |
76.c Refers to the probability of an exposure starting the year in S1 and ending in S2 (Significant Increase in Risk Event)
|
| S2-S1 Rate |
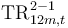 |
76.d Refers to the probability of an exposure starting the year in S2 and ending in S1
|
| S1-S2 ECL |
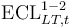 |
76.e The loss associated with the S1-S2 flows for the purposes of the lifetime ECL calculation
|
| S2-SX ECL |
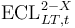 |
76.f Refers to the lifetime expected loss rate for all exposures that start the year in S2 regardless of when and where they transition or if they transition to another stage at all
|
| S3 ECL |
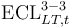 |
76.g Refers to the lifetime expected loss associated with all exposures that start the year in S3. Note that S3 exposures cannot transition to another stage, because of the ‘no cure’ constraint.
|
| S1 LGD |
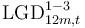 |
76.a Refers to the LGD associated with S1 PD
|
| S2 LGD |
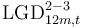 |
76.b refers to the LGD associated with S2 PD
|
| S2-S3 LGD |
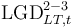 |
The loss associated with the S2-S3 flow for the purposes of the lifetime ECL calculation
|
| Funded collateral (available) |
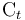 |
Covers all funded collateral, including real estate property, that is available to cover the exposure (Exp) or stock of defaulted exposures (Def Stock) as defined above. Only CRR/CRD eligible collateral and only the bank’s share of collateral (in case collateral is assigned to several debtors) is to be reported. No regulatory haircuts should be applied. Banks are required to provide detailed information on how the collateral values have been determined and how often appraisals are refreshed
|
| Cure rates |
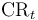 |
Not observed values, but forecasted values affecting LGD estimation in 2017 and in the projected period across both scenarios. While the impact of cures for reducing projected exposures S3 should not be considered for the purpose of this exercise, assumed cure rates are an important component of the LGD estimations. In doing so, banks are required to model cure rates when estimating PDs and LGDs, and report them in the template CSV_CR_SCEN according to the definitions below in a manner that is consistent with the prescribed definitions of each of the stages and LGD. In case a bank does not explicitly calculate cure rates due to its methodological approach, it will be required to outline its calculations of each LGD in more detail in the accompanying note. The following definition applies: Cure(t) is the component of the LGD(t) calculation that corresponds to the assumptions made for the cumulative proportion of existing or projected S3 exposures that cure (through repayments) with zero loss in all years following year t. This naturally depends on the characteristics of the loans at time t.
|
Exposure Stocks
Impairment Stocks
| Term |
Formula |
Definition / Notes
|
| Initial Stock of provisions (Prov Stock) |
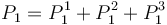 |
62. The starting values of the Stock of provisions must be the accounting figures as of 1 January 2018 in accordance with the IFRS 9 accounting framework to which the reporting entity is subject as listed in columns 030, 060, 070, 080, 090 of FINREP Table 7 (‘financial assets subject to impairment that are past due or impaired’) and in accordance with Article 34 and Article 110 of the CRR for defaulted exposures. It is the sum of provisions for S1, S2 and S3 assets
|
| Stock of provisions S1 (Prov Stock S1) |
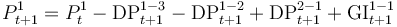 |
Box 3.a Previous S1 stock minus release of provisions from new S3 minus release of provisions from new S2 plus release of provisions from existing S2 plus impairment flow for existing S1
|
| Stock of provisions S2 (Prov Stock S2) |
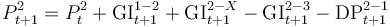 |
Box 3.b Previous Stock S2 plus Gross Imp Flow S1-S2 minus Gross Imp Loss S2-SX minus Gross Imp Flow S2-S3 minus release of provisions from S2
|
| Stock of provisions S3 (Prov Stock S3) |
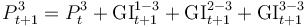 |
Box 3.c Previous Stock S2 plus Gross Imp Flow S1-S3 plus Gross Imp Loss S2-S3 plus Gross Imp Flow S3-S3
|
Exposure Flows
| Term |
Formula |
Definition / Notes
|
| S1-S3 flow |
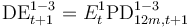 |
56. Measures the amount of exposures that entered into S3 during a given year out of those that were S1 at the start of the period.
|
| S2-S3 flow |
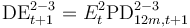 |
56. Measures the amount of exposures that entered into S3 during a given year out of those that were S2 at the start of the period.
|
| S3 flow (SX-S3 Flow) |
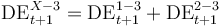 |
55., 56. Measures the amount of exposures that entered into S3 during a given year out of those that were performing (i.e., S1 or S2) at the start of the period. It must include all S3 events that occur during a year. Exposures that enter into S3 several times in 2017 must be reported once. Should be further split into S3 flow S1 to S3 (S1-S3 Flow) and S3 flow S2 to S3 (S2-S3 Flow) based on classification — as either S1 or S2 — of the exposure at the beginning of the period. S3 flow (SX-S3 Flow) should equal the sum of S3 flow from S1 (S1-S3 Flow) and S3 flow from S2 (S2-S3 Flow)
|
| S2-S1 flow |
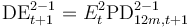 |
57. Measures the amount of exposures that return to S1 during a given year out of those that were S2 at the start of the period. Transitions from S3 to S1 are not permitted in the stress test methodology
|
| S1-S2 flow |
 |
54. Box 6 Measures the amount of exposure that experiences a SICR event (from S1 to S2) during a given year out of those that were S1 at the start of the period.
|
Gross Impairment Flows
| Term |
Formula |
Definition / Notes
|
| Gross impairment loss new S3 (Gross Imp Flow New SX-S3) |
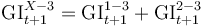 |
64., Box 8 Gross Impairment Flow new S3 is the sum of Gross Impairment loss S1 to S3 (Gross Imp Flow S1-S3) and Gross Impairment loss new S2 to S3 (Gross Imp Flow S2-S3).
|
| Starting Gross Imp Flow New SX-S3) |
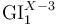 |
63. The starting values of the Gross impairment loss new S3 (Gross Imp Flow New SX-S3) must be the accounting flow figures as of end-2017, defined on the basis of ‘impairment on (non-)financial assets’ (FINREP, table 16.7, column 010; reported year-to-date – i.e. for the starting value provisions that have been set aside in 2017). However, there are two important adjustments to the FINREP figure: (i) the flow should be reported for new S3 assets only (defined as in paragraph 51), and (ii) the flow figures should also include direct write-offs or charge-offs of securities or other assets whose book value is reduced without creating a provision. The guiding principle for this figure is a point-in-time impairment flow, capturing all credit risk-related adjustments, regardless of whether those take the form of provisions or not. The impairment loss should correspond to total impairments of new S3 assets and not only to the additional ones accumulated during the year 2017 – i.e. the stock of impairments that existed at the beginning of the period for these new S3 assets should be included
|
| Gross impairment loss new S1-S3 (Gross Imp Flow New S1-S3) |
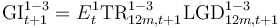 |
67., Box 8 Gross Impairment Flow new S3 from assets that were S1 at start of period.
|
| Gross impairment loss new S2-S3 (Gross Imp Flow New S2-S3) |
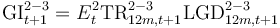 |
69., Box 8 Gross Impairment Flow new S3 from assets that were S2 at start of period.
|
| Gross impairment loss new S1-S2 (Gross Imp Flow New S1-S2) |
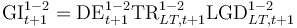 |
66. Box 6 Gross Impairment Flow new S2 from assets that were S1 at start of period. The lifetime ECL is calculated with perfect foresight for the given scenario
|
| Gross impairment loss S2-S1 (Gross Imp Flow New S2-S1) |
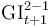 |
68. is a flow that reflects the increase in S1 provisions due to exposure migration from S2. The respective release in lifetime S2 provisions is reflected under Release of S2 provisions from S2-S1 flows. The net flow is therefore given by subtracting Release of S2 provisions from S2-S1 flows from the formula above
|
| Gross impairment loss S2 (Gross Imp Flow S2-SX) |
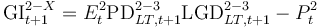 |
70., Box 7 This is a flow variable analogue to Gross Imp Flow SX-S3, but defined for S2 assets at the beginning of each period. Banks are required to reflect the full impact of the scenario (with perfect foresight) on S2 assets as soon as they become subject to lifetime ECL. For exposures that begin the stress test in S2 this means that all impairment charges will occur in year 1 with a portion subsequently transitioning to S3 in the following years as the exposures enter S3, i.e. the lifetime ECL for S2 exposures includes all expected credit losses. The increase of provisions against S2 assets will therefore come from the migration of exposures from S1 to S2 (while a decrease will come from the migration of S2 loans to S3 or S1). This means that this flow should be zero in years 2 and 3 (with additional provisions on S2 assets coming as they migrate from S1 and receive a provision with perfect foresight)
|
| Gross impairment loss S3 (Gross Imp Flow S3-S3) |
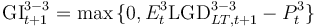 |
71. Box 9 This is a flow variable analogue to Gross Imp Flow SX-S3, but defined for S3 assets at the beginning of each period. In addition to assumed cure rates, impairment loss for S3 assets can be explained by other components such as the ones defined below. Banks are required to report these components in the template CSV_CR_SCEN if their models allow for their computation
|
| Gross impairment loss S1-S1 (Gross Imp Flow S1-S1) |
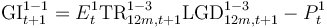 |
65. Box 5 This is a flow that reflects the increase in S1 provisions for assets that start and end the period in S1. It reflects for example, changes in ECL due to macroeconomic scenario changes or rating migrations
|
Net Impairment Flows
| Term |
Formula |
Definition / Notes
|
| Net impairment loss new S3 (Net Imp Flow SX-S3) |
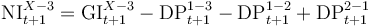 |
The Gross impairment loss new S3 net of 1) the release of provisions from S1 assets caused by the outflow of S3 exposures and S2 exposures and 2) plus the increase in S1 provisions as loans flow from S2 to S1
|
| Net impairment flow S1-S3 (Net Imp Flow S1-S3) |
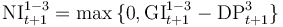 |
|
| Release of S1 provisions from new S1-S3 flows |
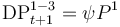 |
73., Box 4 Psi is the share of Prov Stock non-defaulted S1 (t) which is linked to initially S1 assets at t, and which enter into S3 at t+1. At a maximum, alpha can be equal to the share of S1 assets at t, which enter into S3 at t+1, i.e. 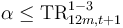
|
| Release of S1 provisions from new S1-S2 flows |
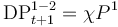 |
72., Box 4 Chi is the share of Prov Stock non-defaulted S1 (t) which is linked to initially S1 assets at t,
and which enter into S2 at t+1. At a maximum, chi can be equal to the share of S1 assets at t, which enter into S2 at t+1, i.e. 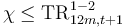
|
| Release of S1 provisions from S2-S1 flows |
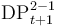 |
74. This is a flow variable which measures the reduction in Prov Stock S2 caused by transitions from S2 to S1 (S1 Flow) when exposures return to 12 month expected losses rather than lifetime expected losses. The increase in provisions for S1 caused by transitions from S2 to S1 should be included as part of release of provisions from S1
|