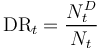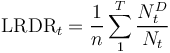Default Rate
Contents
Definition
Default Rate (also Default Frequency) in the context of Credit Risk management is an empirically measured Credit Event realization rate. It is the rate at which loans or other credit assets in a pool default.
Defining the default rate more precisely requires specifying a number of choices as outlined below.
Measurement Choices
Time Horizon
This is simply the time period over which default events are cumulated in order to produce a rate. Depending on the frequency of events it can be anything from monthly to annual. Too short a horizon may produce significant numbers of zero observations, whereas too long a horizon may hide important rate variability information
Volume Based versus Count Based
- A credit event is always associated with a legal entity. Count based approaches focus on the number of legal entities defaulting per period
- A credit event is also always associated with an exposure at risk (although the definition of that may vary). Volume based approaches focus on the size of debt defaulting per period
Cohort versus Run Rate
Defining a default rate requires a precise definition of the population (credit portfolio) being observed. Because credit portfolios are generally evolving, there are two main ways of defining the population over which the default rate is aggregated
- Cohort method, identifying and tracking entities as sets (cohorts) with common time-point of entry into the portfolio
- Run rate method, identifying and tracking all entities that are in the portfolio at a given start time-point
The cohort method is used when trying to create credit risk models that focus on intrinsic borrower characteristics and isolate with higher precision e.g. the effect of the external economic environment. The run rate methods is used when the default rate level or volatility of the actual managed portfolio is the metric of interest
Treatment of Competing Risks
Depending on the context of measurement, a variety of factors (Competing Risks) may modify the number of entities in the measurement portfolio due to causes unrelated to credit risk
- Prepayments / Repayments
- Lack of monitoring / rating[1]
Statistically such effects amount to Risk Sensoring and in cases where they are material in comparison with the typical default rates may need particular attention
Formula
For suitably defined outstanding total count Nt and defaulted NtD count, the default rate for an observation period t is simply the ratio:
NB: A similar ratio can be defined in terms of total outstanding exposure instead of count.
The Long-run Default Rate is given by the average over the entire observation window (composed of n equal periods)[2]
Regulatory Requirements
For the calculation of the one-year default rate and observed average default rates, institutions should adopt the following list[3],[4] .
Scope and Frequency
The observed one year default rates within the historical observation period at least quarterly. The observed average of one-year default rates (‘observed average default rate’) should be calculated for each rating grade or pool and additionally for the type of exposures covered by the relevant PD model as well as for any relevant calibration segment.
For retail exposures and when the definition of default is applied at facility level the calculation can be applied at facility level.
Exposures for which there is no commitment (considering on-balance sheet exposures, off-balance sheet items and unadvised limits) at reference date should be excluded from the calculation of the default rate. Conversely, if there is an exposure at default (EAD) estimate, then these exposures should be included in the calculation of the default rate.
Numerator and Denominator
- The denominator consists of the number of non-defaulted obligors with any credit obligation observed at the beginning of the one-year observation period; in this context a credit obligation refers to both of the following:
- any on balance sheet item, including any amount of principal, interest and fees;
- any off-balance sheet items, including guarantees issued by the institution as a guarantor.
- that the numerator includes all those obligors considered in the denominator that had at least one default event during the one-year observation period.
Where the one-year default rate is calculated by rating grade or pool, the denominator should refer to all obligors assigned to a rating grade or pool at the beginning of the observation period. Where the one-year default rate is calculated at the portfolio level, the denominator should refer to all obligors assigned to the relevant Calibration Segment at the beginning of the observation period.
Multiple Defaults
Institutions should ensure that each defaulted obligor is counted only once in the numerator and denominator of the one-year default rate calculation, even where the obligor defaulted more than once during the relevant one-year period.
Overrides
When assigning the obligors or exposures to grades or pools for the purpose of the one-year default rate calculation, institutions should take Overrides into account, but they should not reflect in this assignment any substitution effects due to credit risk mitigation, nor any ex post conservative adjustments.
Left Censoring
Institutions should calculate the one-year default rate also for the subset of obligors with any credit obligation that did not have a rating at the start of the relevant observation period, but which were within the range of application of the model under consideration (‘missing ratings’), even if these obligors were assigned to a rating grade or pool in a conservative manner for the purpose of calculation of own funds requirements.
Obligors whose ratings are based on missing or partly missing information or where the rating is outdated but still deemed valid by the institution should not be considered as missing ratings.
Discontinued Ratings
An obligor has to be included in the denominator and, where relevant, numerator, also in the case of a migration to a different rating grade, pool or rating model, rating system or approach to calculation of capital requirements within the observation period or where the corresponding credit obligations were sold, written off, repaid or otherwise closed during the observation period. Institutions should analyse whether such migrations or sales of credit obligations bias the default rate and, if so, they should reflect this in an appropriate adjustment and consider an adequate MoC.
Overlapping Windows
Institutions should choose an appropriate approach between an approach based on overlapping and an approach based on non-overlapping one-year time windows, to calculate the observed average default rate based on a documented analysis. This analysis should include at least the following:
- an analysis of possible bias due to the proportion of short-term and terminated contracts that cannot be observed during the relevant one-year periods;
- an analysis of possible bias due to the specific calculation dates chosen;
- for institutions using overlapping one-year time windows, an analysis of potentially significant bias due to implicit over-weighting of the overlapping time period;
- an analysis of potentially significant bias due to seasonal effect related to the chosen calculation dates.
One-year time windows should preferably be used when the analysis performed reveals any of the following:
- the proportion of short-term and terminated contracts and/or the respective distribution of default rates is not stable over time;
- the observed average default rate using overlapping one-year time windows is significantly different from the observed average default rate using non-overlapping one-year time windows;
- there is a significant variation between the observed average default rates calculated using non-overlapping one-year time windows on different reference calculation dates within a year.
Use of Arithmetic Average
Institutions should calculate the observed average default rates as the arithmetic average of all one year default rates. In the case of PD models for retail exposure class institutions may calculate the observed average default rate as a weighted average of one-year default rates where an institution does not give equal importance to historic data because more recent data is a better predictor of losses in accordance with Article 180(2)(e) of Regulation (EU) No 575/2013
External Risk Data
Institutions should estimate PDs taking their own internal data into consideration. The more internal default experience an institution has, the less importance it needs to give to external data. In cases where institutions use external or pooled data series to complement their internal data for the purpose of PD estimation, they must ensure that these data are representative.
Institutions should also ensure that the average observed default rates from external/pooled data are calculated separately from those based on internal data. The direction and magnitude of the differences between these averages should be properly analysed and documented when calibrating the model, including the adequacy of the MoC considered, and duly followed up in the review of estimates.
References
See Also
- Probability of Default
- Probability of Default versus Default Rate
- Default Rate Volatility
- Incremental Default Rate
Disclaimer
This entry annotates a FIBO Ontology Class. FIBO is a trademark and the FIBO Ontology is copyright of the EDM Council, released under the MIT Open Source License. There is no guarantee that the content of this page will remain aligned with or correctly interprets the concepts covered by the FIBO ontology.
| IsDefinedBy URI of an entity that is defined via an imported vocabulary. | https://spec.edmcouncil.org/fibo/ontology/MD/DebtTemporal/DebtPricingYields/index-en.html + |