Adjacency Matrix
Definition
Adjacency is the graph theoretic representation of the fact that two entities, represented by graph nodes, are directly related, tied, or connected with one another.
An Adjacency Matrix in the context of Input-Output Analysis is a Boolean matrix (composed of zeros and ones) representing the Supply Chain network connecting economic activities without specific regard to the actual magnitudes (e.g., volumes or monetary values) being exchanged. The sectoral dependencies represented in an input-output table (IOT) can be converted into an adjacency matrix representing the supply chain network that connects economic activities.
A Weighted Adjacency Matrix is instead a matrix composed or numerical values (real numbers) representing values attached to the edges of a Weighted Graph. The transactions matrix Z can be thought of as a weighted adjancency matrix.
Formula
The general approach[1] for the construction of an adjacency matrix is to perform is a binary (Boolean) transformation on either the transactions matrix Z or the coefficients matrix (A) to generate matrices with “1” in cells for which 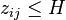 (or
(or 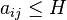 ) and “0” elsewhere (where H is a suitable threshold).
) and “0” elsewhere (where H is a suitable threshold).
Usage
Given entities i and j in a set of N agents (nodes, entities, sectors etc.) and an adjacency matrix 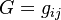 of arcs (edges, links) denoting the existence of relations from i to j, agents i and j are adjacent if there exist either of the two arcs from i to j or from j to i.
of arcs (edges, links) denoting the existence of relations from i to j, agents i and j are adjacent if there exist either of the two arcs from i to j or from j to i.
The adjacency matrix G can then be analysed using techniques from graph and network theory to reveal economic structure and other features of the system being analysed.
See Also
Further Resources
References
- ↑ R.E. Miller and P.D. Blair, Input-Output Analysis: Foundations and Extensions, Second Edition, Cambridge University Press, 2009