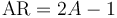Accuracy Ratio
Contents
Definition
Accuracy Ratio (AR) is a summary quantitative measure of the Discriminatory Power in classification models (e.g. Credit Scoring Models). The AR measure expresses the ratio of the area above and under the power curve (also cumulative accuracy profile (CAP)) of the model under consideration versus the "perfectly" discriminating model. (See also: Receiver Operating Characteristic)
The ratio AR can take values between zero and one. The closer AR is to one, i.e. the larger the excess surface covered by the CAP curve, the higher the discriminative power of the classification system.
The accuracy ratio is sometimes also denoted as the Gini Coefficient yet it should not be confused with the more common use of that term to measure inequality.
Formula
Mathematically the above definition is expressed as
where aR and aP are the areas for the actual and perfect model respectively.
An alternative expression is in terms of the probabilities that the score of defaulted entities is above or below those of non-defaulted entities:
The area A under the ROC curve and the CAP accuracy ratio AR are connected by means of the linear transformation[1]
Confidence Intervals
The AR is a statistical metric subject to estimation noise due to sample size. In general, two procedures can be used to calculate confidence levels:
- Approximate analytical estimation of confidence levels under some distribution assumption
- Heuristic estimation by means of resampling (bootstraping)
Issues and Challenges
In addition to the level of the AR measure, its stability is also a significant factor for assessing the quality of a credit risk system with respect to disciminatory power. Such stability concerns both
- the classification system applied to unknown data (out-of-sample validation)
- the classification system applied to different (longer) forecasting horizons
See Also
Open Source Software
References
- ↑ BIS Working Paper No. 14 Studies on the Validation of Internal Rating Systems
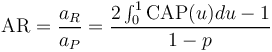
![\mbox{AR} = P[S_{D} < S_{N}] - P[S_{D} > S_{N}]](https://www.openriskmanual.org/wiki/images/mathdata/f/e/5/fe5df6b6f4ecce79e7557e347bb12b23.png)