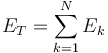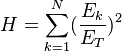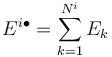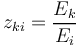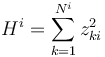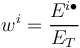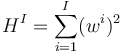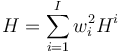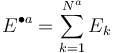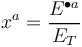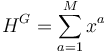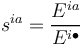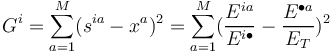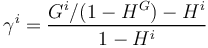Ellison-Glaeser Index
Contents
Definition
The Ellison-Glaeser Index (EG) is an index developed for the assessment of industrial agglomeration[1]
Details
The calculation process for the EG index is detailed here (the terminology and steps are adjusted versus the original publication to typical Concentration Risk applications)
Exposures
We have N exposures 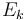 summing up to a total exposure of
summing up to a total exposure of
Each exposure is associated with one industry (business sector) and one geography. The total HHI index capturing single exposure concentration across the entire portfolio is
Business Sectors
We have I industries (business sectors)  . Each industry comprises of
. Each industry comprises of 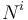 exposures. The total exposure per industry is
exposures. The total exposure per industry is
where the bullet denotes the implied summation over all areas. The fraction of each exposure within an industry is
The HHI index within each industry is defined as
The fraction of each industry as part of the total exposure is
The HHI index capturing concentration in the distribution of the different industry sectors
The aggregate HHI is connected with the industry specific indexes via
Geographic Areas
We have M areas (countries or regions) 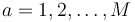 . Each area comprises of
. Each area comprises of 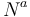 exposures. The total exposure per area is
exposures. The total exposure per area is
The fraction of each area as part of the total exposure is
The geographic concentration is captured by an HHI type metric
Raw Concentration Metric
Within each area, an industry comprises of 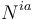 exposures, summing up to a total of
exposures, summing up to a total of 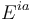 for each industry / area combination. The allocation of industry exposure to areas is given by
for each industry / area combination. The allocation of industry exposure to areas is given by
An (ad-hoc) metric capturing industry exposure concentration per area
This metric is zero when industrial exposure in an area as a fraction of the total in that industry is the same as the fraction of all industrial exposure in that area over all exposure.
EG Index per industry
The EG industrial concentration index (per industry i) is given by
Usage
None
Variations
None
Issues and Challenges
- The setup for the calculation of the EG index implies that the geographical distribution of exposures is given (i.e. it does not measure geographic distribution per se, but the relative concentration of industrial exposure given the overall geographical distribution
- The EG index is sensitive to the definition of geographical regions
Implementations
Open Source implementations of the Ellison-Glaeser index are available in
- The Python library Concentration Library
- The Python spatial analysis library PySAL
See Also
None
References
- ↑ Ellison, Glaeser, Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach, 1997