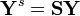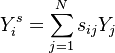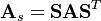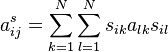Difference between revisions of "Aggregation Matrix"
Wiki admin (talk | contribs) (Created page with "== Definition == '''Aggregation Matrix''' in the context of Input-Output Analysis is a Boolean matrix (composed of zeros and ones) that aim to produce a coarse-grained ver...") |
Wiki admin (talk | contribs) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
| − | '''Aggregation Matrix''' in the context of [[Input-Output Analysis]] is a Boolean | + | '''Aggregation Matrix''' (also ''Summation Matrix'') in the context of [[Input-Output Analysis]] is a [[Boolean Matrix]] that aims to produce a coarse-grained version of a more granular [[Input-Output Model]]. |
| + | |||
| + | Aggregation can be for example along sectoral or regional dimensions. | ||
| + | |||
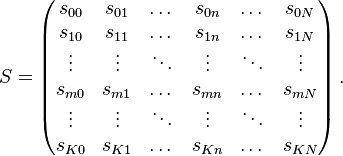
| + | Vectors and Matrices can be aggregated by multiplying with the aggregation matrix. Mathematically a aggregation matrix S is a <math>K \times N</math> matrix, where each value <math>s_{mn}</math> is either zero or one. The aggregation matrix has in total N non-zero values. | ||
| + | |||
| + | :<math>S=\left(\begin{matrix} | ||
| + | s_{00} & s_{01} & \dots &s_{0n} & \dots & s_{0N} \\ | ||
| + | s_{10} & s_{11} & \dots &s_{1n} & \dots & s_{1N} \\ | ||
| + | \vdots & \vdots & \ddots &\vdots & \ddots & \vdots \\ | ||
| + | s_{m0} & s_{m1} & \dots &s_{mn} & \dots & s_{mN} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots& \ddots & \vdots \\ | ||
| + | s_{K0} & s_{K1} & \dots & s_{Kn} & \dots & s_{KN}\\ | ||
| + | \end{matrix}\right). | ||
| + | </math> | ||
| + | |||
| + | An aggregation matrix with K rows and N columns is used to aggregate a dimension of size N into a smaller dimension of size K. The N non-zero (unit) values select and group the elements of the vector or matrix that is to be aggregated. | ||
| + | |||
| + | === Vector Quantity Aggregation === | ||
| + | A vector Y of dimension N is aggregated into a vector K through its pre-multiplication with the aggregation matrix. | ||
| + | |||
| + | :<math> | ||
| + | \mathbf{Y}^{s} = \mathbf{S} \mathbf{Y} | ||
| + | </math> | ||
| + | |||
| + | or more explicitly: | ||
| + | |||
| + | :<math> | ||
| + | Y^{s}_{i} = \sum_{j=1}^{N} s_{ij} Y_j | ||
| + | </math> | ||
| + | |||
| + | === Matrix Quantity Aggregation === | ||
| + | |||
| + | A matrix of dimension N x N is aggregated into a K x K matrix through its pre-multiplication with the aggregation K x N matrix and the post-multiplication with the (N x K) aggregation matrix transpose. | ||
| + | |||
| + | :<math>\mathbf{A}_{s} = \mathbf{S} \mathbf{A} \mathbf{S}^T</math> | ||
| + | |||
| + | or more explicitly: | ||
| + | |||
| + | :<math> | ||
| + | a^{s}_{ij} = \sum_{k=1}^{N} \sum_{l=1}^{N} s_{ik} a_{lk} s_{il} | ||
| + | </math> | ||
| + | |||
== See Also == | == See Also == | ||
* [[Aggregation Bias]] | * [[Aggregation Bias]] | ||
| + | * [[Summation Vector]] | ||
| + | |||
| + | == Further Resources == | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=70 Crash Course on Input-Output Model Mathematics] | ||
| + | * [https://www.openriskacademy.com/course/view.php?id=64 Introduction to Input-Output Models using Python] | ||
| + | |||
[[Category:EEIO]] | [[Category:EEIO]] | ||
Latest revision as of 18:50, 20 November 2023
Contents
Definition
Aggregation Matrix (also Summation Matrix) in the context of Input-Output Analysis is a Boolean Matrix that aims to produce a coarse-grained version of a more granular Input-Output Model.
Aggregation can be for example along sectoral or regional dimensions.
Vectors and Matrices can be aggregated by multiplying with the aggregation matrix. Mathematically a aggregation matrix S is a 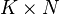 matrix, where each value
matrix, where each value 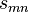 is either zero or one. The aggregation matrix has in total N non-zero values.
is either zero or one. The aggregation matrix has in total N non-zero values.
An aggregation matrix with K rows and N columns is used to aggregate a dimension of size N into a smaller dimension of size K. The N non-zero (unit) values select and group the elements of the vector or matrix that is to be aggregated.
Vector Quantity Aggregation
A vector Y of dimension N is aggregated into a vector K through its pre-multiplication with the aggregation matrix.
or more explicitly:
Matrix Quantity Aggregation
A matrix of dimension N x N is aggregated into a K x K matrix through its pre-multiplication with the aggregation K x N matrix and the post-multiplication with the (N x K) aggregation matrix transpose.
or more explicitly: